Consistent Hashing
About four years ago at Yipit.com we had to add nodes to our memcached cluster to increase its caching capacity and availability, but we were using a memcached client that partitioned data across nodes using the hash partitioning algorithm, and thus, most of the cache would become invalid when the number of nodes changes. There are multiple algorithms to partition data across a cluster but this article will cover only hash partitioning and consistent hashing in the context of caching. The terms node and server are used interchangeably in this article.
For more details about other partitioning algorithms and their implementations, check out chapter 8 of my book Redis Essentials.
Data Partitioning
When you’re dealing with a significant amount of data to store or cache, it’s a common practice to have multiple data nodes to have more storage capacity, achieve higher availability, or balance request load.
With multiple data nodes, the client has to decide what node will receive the request. To minimize cache misses, you should route requests for the same key to the same node. For example:
client.set("user-1", "name-1"): changeserver-1client.get("user-1"): retrieve fromserver-1–> FOUNDclient.set("user-2", "name-2"): changeserver-2client.get("user-2"): retrieve fromserver-2–> FOUND
If you can’t ensure that requests to user-1 always get routed to server-1, you’ll create unnecessary cache misses. For example:
client.set("user-1", "name-1"): changeserver-1client.get("user-1"): retrieve fromserver-2–> CACHE MISS
To ensure routing consistency, you’ll need to pick a deterministic algorithm. Ideally, something that is flexible enough that allows you to change the size of the cluster in the future without creating too many cache misses.
Hash Partitioning
The hash partitioning algorithm is straightforward: you generate a hash of the key you want to store and calculate the modulo of that with the number of servers (hash(k) mod n, where k is the key and n is the number of servers).
Assuming you want to store key with value value, and you have multiple server objects in servers, the following code would find the right server to store key:
def set(key, value, servers):
n = len(servers)
index = hash(key) % n
servers[index].set(key, value)
The problem with this algorithm is that if you change the number of servers, most of the modulo results are going to change and you will end up with a lot of cache misses.
For the following examples, assume your cache cluster has three nodes and you are storing keys key1 and key2:
# base case
>>> n = 3
>>> hash('key1') % n
1
>>> hash('key2') % n
0
The key key2 will be stored on the first server (servers[0]) and key1 on the second server (servers[1]).
However, those values change if the number of nodes is modified:
# adding one node (3 + 1)
>>> n = 4
>>> hash('key1') % n
2
>>> hash('key2') % n
1
# removing one node (3 - 1)
>>> n = 2
>>> hash('key1') % n
0
>>> hash('key2') % n
1
As you can see, changing the number of nodes invalidates the cache of both key1 and key2. Hash partitioning works in many cases and it’s simple to implement, but you’ll get penalized if the number of nodes ever change.
Consistent Hashing
From Wikipedia:
Consistent hashing is based on mapping each object to a point on the edge of a circle (or equivalently, mapping each object to a real angle). The system maps each available machine (or other storage bucket) to many pseudo-randomly distributed points on the edge of the same circle.
I like what we wrote about consistent hashing for the book and decided to copy it here. The following is an excerpt from my book Redis Essentials, chapter 8, subsection Consistent Hashing:
We explained how hash partitioning works before. Its main downside is that adding or removing nodes from the list of servers may have a negative impact on key distribution and creation. If Redis is used as a cache system with hash partitioning, it becomes very hard to scale up because the size of the list of Redis servers cannot change (otherwise, a lot of cache misses will happen).
Some researchers at MIT were trying to solve the problem with hash partitioning and caching that we just described, and they came up with the concept of consistent hashing. They wanted a different technique to route keys that would affect only a small portion of data when the hash table was resized.
Consistent hashing, in our context, is a kind of hashing that remaps only a small portion of the data to different servers when the list of Redis servers is changed (only K/n keys are remapped, where K is the number of keys and n is the number of servers).
For example, in a cluster with 100 keys and four servers, adding a fifth node would remap only 25 keys on an average (100 divided by 4). Consistent hashing is also known as a hash ring.
The technique consists of creating multiple points in a circle for each Redis key and server. The appropriate server for a given key is the closest server to that key in the circle (clockwise); this circle is also referred to as “ring.” The points are created using a hash function, such as MD5.
In order to understand the next examples, assume the following:
- Servers available:
- server-1,
- server-2, and
- server-3
- Key to be stored:
- testkey-1,
- testkey-2,
- testkey-3, and
- testkey-4
- Points per server: 1
Assume that there is a hash function that returns the following values for the servers:
hash("server-1") = 3
hash("server-2") = 7
hash("server-3") = 11
The same hash function returns the following values for the keys:
hash("testkey-1") = 3
hash("testkey-2") = 4
hash("testkey-3") = 8
hash("testkey-4") = 12
The following diagram shows the circle with the previous hashes:
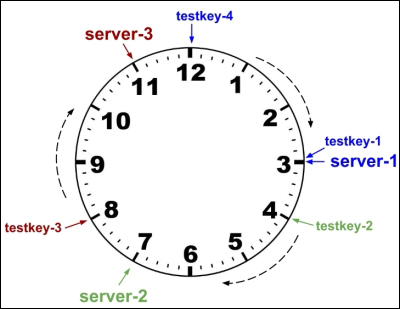
In this hypothetical example, the mapping is as follows:
testkey-1maps toserver-1. They have to the same value of 3.testkey-2maps toserver-2. This is the next server available with a value greater than or equal to 4, and the key distribution moves clockwise.testkey-3maps toserver-3. This is the next server available with a value greater than or equal to 8, moving clockwise again.testkey-4maps toserver-1. There is no server with a hash greater than or equal to 12. Thus,testkey-4falls back to the first node in the ring.
The previous example shows how consistent hashing can be used to route Redis keys to a cluster of Redis servers (the hash values are hypothetical and are meant only to exemplify the concept). In the real world, it is better to use multiple points for each server, because that way it is easier to distribute keys and keep the ring balanced. Some libraries use as few as three points per server, while others use as many as 500.
The book has a Node.js basic implementation of consistent hashing, it’s available on Github: https://github.com/redis-essentials/book/blob/master/chapter%208/consistenthashing.js
When you want a more robust alternative to hash partitioning, consistent hashing is my recommendation. It’s not as straightforward to implement as hash partitioning, but there are multiple libraries that can help you. The earlier you switch algorithms, the fewer issues you’ll have in the future. You’ll regret not changing your partitioning strategy early on when your app is under heavy load and changing the number of cache nodes adds gasoline to the fire.
If you want to read more about consistent hashing, I recommend the following resources:
Conclusion
Back in 2014, we were using Django’s default memcached client and we switched to Django Memcache Hashring client. The transition has a cost: lots of cache misses initially. After a while, it will stabilize and enable you to change the number of nodes without too many cache misses.
Next time you end up with a routing problem with a cache cluster, consider the Consistent Hashing algorithm.